My Neobux Portal
Can You Solve These Wheel of Fortune Style Puzzles Quiz Answers from Offer 100% correct answers. Complete your quiz offer with 100% accuracy and get credited.
Quizzes are constantly updated. New questions are added and answers are changed. If you find any questions that are not present here or if your score was not 100% with the answers on our site, please let us know in the form before the comment section with the quiz link. We will update the answers as soon as we can.
Q 1. DO YOU KNOW THE ANSWER TO THIS TRIVIA?
Option:-
Cerebral Aqueduct
Medulla Oblongata
Cerebral Ventricle
Pituitary Gland
Q 2. CAN YOU ANSWER THIS TRIVIA?
Option:-
Captain Planet
Captain Marvel
Captain Britain
Captain America
Q 3. CAN YOU ANSWER THIS TRIVIA?
Option:-
National Council
Federal Council
States General
Supreme Council
Q 4. CAN YOU ANSWER THIS TRIVIA?
Option:-
The Iceman
The Firefighter
The Firehouse
The Fireman
Q 5. DO YOU KNOW THE ANSWER TO THIS TRIVIA?
Option:-
Protasis
Proboscis
Proptosis
Trombosis
Q 6. WHAT IS THE ANSWER TO THIS TRIVIA?
Option:-
Lusitania
Justisia
Carinthia
Lancastria
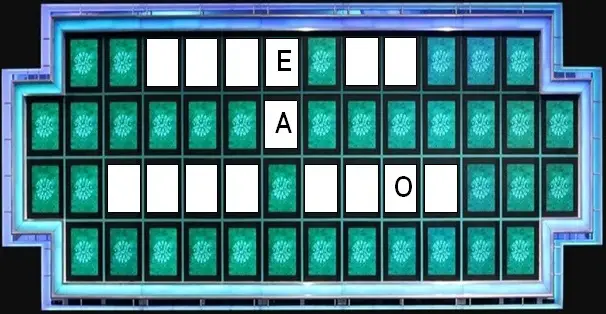
Q 7. WHAT IS THE THIRD MISSING LETTER IN THE PUZZLE?
Option:-
A
C
U
L
Q 8. WHAT IS THE FIFTH MISSING LETTER?
Option:-
E
O
N
T
Q 9. WHAT IS THE THIRD MISSING LETTER?
Option:-
T
P
L
A
Q 10. WHAT IS THE THIRTEENTH MISSING LETTER?
Option:-
E
T
C
A
Q 11. WHAT IS THE EIGHT MISSING LETTER?
Option:-
G
U
D
O
Q 12. WHAT IS THE TENTH MISSING LETTER?
Option:-
N
S
A
I
Q 13. WHAT IS THE FIFTH MISSING LETTER?
Option:-
C
T
A
I
Q 14. WHAT IS THE SECOND MISSING LETTER?
Option:-
T
O
I
R
Q 15. WHAT IS THE FOURTH MISSING LETTER?
Option:-
A
T
I
O
Q 16. WHAT IS THE SECOND MISSING LETTER?
Option:-
O
E
I
A
Q 17. WHAT IS THE ANSWER TO THIS TRIVIA?
Option:-
Activism
Moralism
Optimism
Stoicism
Q 18. CAN YOU ANSWER THIS TRIVIA QUESTION?
Option:-
Schizophrenia
Synesthesia
Hypersomnia
Paresthesia
Q 19. WHAT IS THE ANSWER TO THIS TRIVIA QUESTION?
Option:-
Classical Acting
Meisner Acting
Chekhov Acting
Method Acting
Q 20. DO YOU KNOW THE ANSWER TO THIS TRIVIA?
Option:-
Boomerang Nebula
Footprint Nebula
Butterfly Nebula
Spirograph Nebula
Q 21. DO YOU KNOW THE ANSWER TO THIS TRIVIA?
Option:-
Once in a While
Once in a Pale Moon
Once in a Bare Noon
Once in a Blue Moon
Q 22. ARE YOU FAMILIAR WITH THIS TRIVIA?
Option:-
BlackPearl
Crayon Pop
BlackPink
Playback
Q 23. DO YOU KNOW THE ANSWER TO THIS TRIVIA?
Option:-
Peanut Butter and Jelly
Fried Chicken and Waffles
Mashed Potatoes and Gravy
Burger and French Fries
Q 24. WHAT IS THE ANSWER TO THIS TRIVIA?
Option:-
Uranium
Helium
Indium
Cerium
Q 25. DO YOU KNOW THE ANSWER TO THIS TRIVIA?
Option:-
Composite Numbers
Fibonacci Sequence
Geometric Sequence
Hexagonal Numbers
[adace-ad id=”22311″]
[adace-ad id=”22312″] 
100%! Thank you. xx
Now, this one gives me 95% It’s the same quiz but the questions are randomized it’s confusing ):
Its how they made the quiz. Nothing I can do about it. Try again you probably made a mistake with a question.
Please update the questions
All questions are available from the quiz. The questions order get randomized each time. So match corresponding question and answer accordingly.